SECANTE
El Secante, (abreviado como sec), es la razón trigonométrica recíproca del coseno, o también su
inverso multiplicativo:
En un triángulo rectángulo, es la longitud de la hipotenusa dividida para
la longitud del lado adyacente.

Las
funciones trigonométricas circulares son aquellas que están referenciadas en la
circunferencia. Usamos entonces la llamada circunferencia trigonométrica de
radio unidad que se usa en el estudio de las funciones. De acuerdo con el
cuadrante en el cual se encuentre el lado terminal de ángulo y tomando en
cuenta que la distancia correspondiente a un punto cualquiera al origen de
coordenadas es siempre positivo, las funciones trigonométricas pueden ser
positivas o negativas. En el recuadro que se muestra a continuación podemos ver
que signo corresponde a cada cuadrante si hablamos de secante.
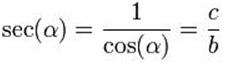
La «secante circular del ángulo a», o, simplemente,
«secante de a»
La función no tiene ceros ya que para que de
existir tendría que poder anularse el numerador de la fracción 1/cos x y eso no
ocurre nunca porque es una constante:
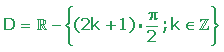
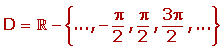
Características
Las características fundamentales de
la función secante son las siguientes:
1) Su dominio es R
- {π/2 + k·π} con k∈Z .
2) Su recorrido
es R - (- 1, 1) .
3) No corta al eje X.
Corta al eje Y en el
punto (0, 1) .
4) Es par, es decir, simétrica
respecto al eje Y.
sec (- x) = sec (x)
5) Tiene infinitos máximos relativos
en los puntos de la forma (π + 2·k·π, -
1) con k∈Z
Tiene infinitos mínimos
relativos en los puntos de la forma (2·k·π, 1) con k∈Z.
6) Es periódica de
periodo 2π .
sec (x) = sec (x + 2π)
7) Tiene asíntotas verticales en los
puntos de la forma x = π/2 + k·π con k∈Z .
8) No está acotada.
Forma geométrica
Sabiendo que

Tenemos que:

Otro planteamiento de
la misma cuestión se hace trazando una perpendicular a r por B, esta perpendicular corta el eje x en J, así tenemos:

Esta solución es
distinta de la anterior.
Ejemplos:
.gif)















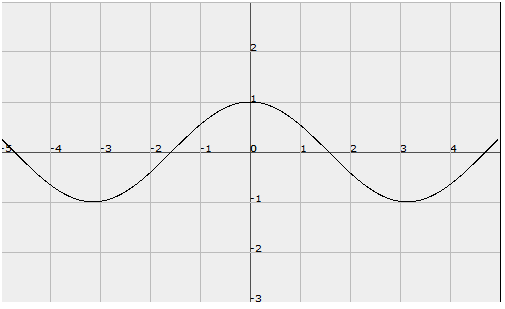

 . Así, se cicla una vez de 0
a
. Así, se cicla una vez de 0
a 