ECUACIONES DE SEGUNDO GRADO
Una ecuación de segundo
grado o ecuación cuadrática de una variable es una ecuación que tiene la expresión general:
Ecuación de segundo grado

donde x es la variable, y a, b y c constantes; a es el coeficiente cuadrático
(distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede
interpretar mediante la gráfica de una función cuadrática, es decir, por una parábola. Esta representación
gráfica es útil, porque las abscisas de las intersecciones o punto de tangencia
de esta gráfica, en el caso de existir, con el eje X son las
raíces reales de la ecuación. Si la parábola no corta el eje X las raíces son
números complejos, corresponden a un discriminante negativo.
 Las ecuaciones de segundo grado y su solución de las ecuaciones se conocen desde la antigüedad. En Babilonia se conocieron algoritmos para
resolverla. Fue encontrado independientemente en otros lugares del mundo. En Grecia, el matemático Diofanto de Alejandría aportó un procedimiento para resolver este tipo de
ecuaciones (aunque su método sólo proporcionaba una de las soluciones, incluso
en el caso de que las dos soluciones sean positivas). La primera solución
completa la desarrolló el matemático Al-Juarismi (o
Al-Khwarizmi según otras grafías), en el siglo IX en su trabajo Compendio de
cálculo por reintegración y comparación, cerrando con ello un problema que se había perseguido
durante siglos. Basándose en el trabajo de Al-Juarismi, el matemático
judeoespañol Abraham bar Hiyya, en su Liber embadorum, discute la
solución de estas ecuaciones. Hay que
esperar a Évariste Galois para conseguir resolver en general las ecuaciones
polinómicas, o saber cuándo son irresolubles por radicales, que viene a ser una
generalización de los métodos de resolución de las ecuaciones de segundo grado.
Las ecuaciones de segundo grado y su solución de las ecuaciones se conocen desde la antigüedad. En Babilonia se conocieron algoritmos para
resolverla. Fue encontrado independientemente en otros lugares del mundo. En Grecia, el matemático Diofanto de Alejandría aportó un procedimiento para resolver este tipo de
ecuaciones (aunque su método sólo proporcionaba una de las soluciones, incluso
en el caso de que las dos soluciones sean positivas). La primera solución
completa la desarrolló el matemático Al-Juarismi (o
Al-Khwarizmi según otras grafías), en el siglo IX en su trabajo Compendio de
cálculo por reintegración y comparación, cerrando con ello un problema que se había perseguido
durante siglos. Basándose en el trabajo de Al-Juarismi, el matemático
judeoespañol Abraham bar Hiyya, en su Liber embadorum, discute la
solución de estas ecuaciones. Hay que
esperar a Évariste Galois para conseguir resolver en general las ecuaciones
polinómicas, o saber cuándo son irresolubles por radicales, que viene a ser una
generalización de los métodos de resolución de las ecuaciones de segundo grado.
Soluciones
de ecuaciones de segundo grado
Para una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones,
no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas (si
los coeficientes son reales y existen dos soluciones no reales, entonces deben
ser complejas conjugadas). Fórmula general para la obtención de raíces:

Se usa ± para indicar las dos soluciones:


Las ecuaciones de
segundo grado se dividen en: ecuaciones completas y ecuaciones incompletas de segundo grado.
1.Ecuaciones
completas de segundo grado
Son aquellos que tienen un
término de segundo grado (es decir, un término «en X2»), un término lineal (es
decir, «en x») y un término independiente, es decir, un número sin x. Un ejemplo de una ecuación de este
tipo es la siguiente:
2×2 – 4x – 3 = 0
Tenga en cuenta que el coeficiente del término cuadrado se
llama generalmente a, el término lineal es llamado por y el independiente se
llama c, de modo que en este caso:
a = 2, b = -4 y c = -3.
Por esta razón, la forma de tipo de estas ecuaciones está
representada por la siguiente expresión general:
ax^2+bx+c=0
2.Ecuaciones
incompletas de segundo grado
Para simplificar, una ecuación de segundo
grado no está completa cuando le falta uno de los tres términos que se han
mencionado que existen en ecuaciones de segundo grado completas. Sí, está claro
que el término cuadrado no puede fallar de lo
contrario, éste no sería una ecuación de segundo grado.
Bien, hay dos tipos
de ecuaciones incompletas de segundo grado: las que carecen del término lineal
(es decir, el término «en x») y las que carecen del término independiente (es
decir, la que no tiene x )
En el primer caso, falta el
término que contiene el coeficiente llamado «b», por lo que la forma de tipo
permanecerá de la siguiente manera:
ax^2 + c = 0
La ecuación cuadrática incompleta, en el segundo caso, falta
el término independiente, es decir, el que contiene el coeficiente llamado «c»,
por lo que la forma del tipo permanecerá
ahora como sigue: ax^2 + bx = 0
La
ecuación de segundo grado: ax2+bx+c=0 puede
tener una, dos o ninguna solución Para averiguarlo sin tener que resolver la
ecuación vamos a recurrir a la discriminante de una ecuación de
segundo grado. El valor del discriminante (al que vamos a llamar D) viene
dado por D = b2 - 4ac
·
Si
D > 0, la ecuación tiene dos soluciones reales distintas.
·
Si D
= 0, la ecuación tiene dos soluciones reales iguales (Una solución
doble).
·
Si
D < 0, la ecuación no tiene solución real.
Ejemplos:
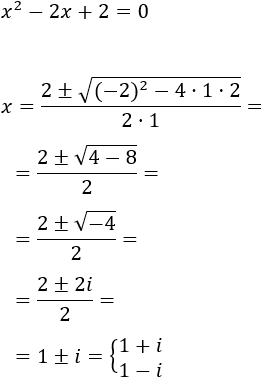

No hay comentarios:
Publicar un comentario