Suma o diferencia de cubos
Recordamos de cocientes notables que:
Recordamos de cocientes notables que:
Pero en la división exacta el dividendo es igual al divisor
multiplicado por el cociente, efectuándolo nos queda:
De donde
se deducen las siguientes reglas:
- La
suma de dos cubos perfectos se descompone en dos factores, el primero es
la suma de sus raíces cúbicas, y el segundo se compone de el cuadrado de
la primera raíz menos el producto de ambas raíces más el cuadrado de la
segunda raíz.

- La diferencia de dos cubos perfectos se descompone en dos factores, el primero es la diferencia de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz más el producto de ambas raíces mas el cuadrado de la segunda raíz.
La suma o diferencia de dos cubos puede factorizarse en un producto de
un binomio por un trinomio.
Esto
es,  y
y  .
.
 y
y  .
.
Una
mnemónica para los signos de la factorización es la palabra "SOAP",
las letras indican "Same sign (mismo signo)" como en el
medio de la expresión original, "Opposite sign (signo opuesto)", y "Always Positive
(siempre positivo)".
Ejemplo explicativo: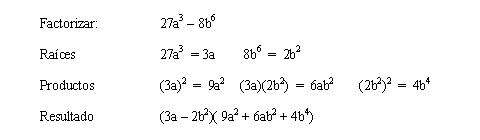
Ejemplos:


Factorice  .
.
 .
.
Intente escribir cada uno de los términos como un cubo de una expresión.

Use la factorización de la suma de cubos para reescribir.


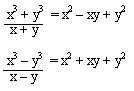
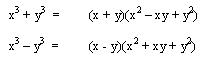
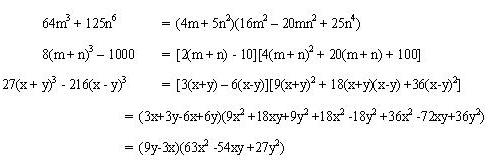

No hay comentarios:
Publicar un comentario