SENO
El seno de un ángulo α de
un triángulo rectángulo se
define como la razón entre el cateto opuesto (a) y la hipotenusa (c).
Es una de las razones trigonométricas.
Se llaman razones porque se expresan como el cociente de dos de los lados
del triángulo rectángulo.
Su abreviatura son sen o sin (del
latín sinus).
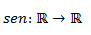
Es decir, que pertenece al conjunto de los
números reales, y su solución es otro número real, que se expresa como f(x)=
sen(x), es por tanto, una aplicación de la razón trigonométrica seno a una
variable independiente, que se suele expresar en radianes
Cabe destacar que los valores
del seno siempre variarán entre -1 y 1, como se puede ver en la siguiente
gráfica:
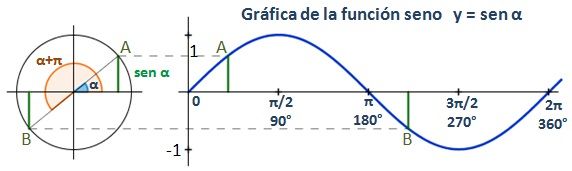
Además, se puede ver que es una función impar,
ya que sus elementos opuestos tienen imágenes opuestas (el seno de 30 es 1/2, y
el de -30 es -1/2) y también continua en todo su recorrido
.
Nota: para recordar que tiene
imágenes opuestas, podéis quedaros con la idea de que es como una ola, que
viene y va, estrellándose contra la arena, para volver a surgir de nuevo.
Si nos fijamos atentamente,
veremos que el seno no es más que el cateto opuesto al ángulo, partido de la
hipotenusa de un triángulo rectángulo. Si vamos rotando ese triangulo
imaginario en esa circunferencia, nos irá dando los distintos valores de los
ángulos del seno.

Características
Las características fundamentales de
la función seno son las siguientes:
1) Su dominio es R y es continua.
2) Su recorrido
es [- 1, 1] ya que - 1 ≤ sen
x ≤ 1 .
3) Corta al eje X en los
puntos k·π con k∈Z .
Corta al eje Y en el
punto (0, 0) .
4) Es impar, es decir, simétrica
respecto al origen.
sen (- x) = - sen (x)
5) Es estrictamente
creciente en los intervalos de la forma (a,
b) donde a = - π/2 + 2·k·π y b = π/2 + 2·k·π siendo k∈Z .
Es estrictamente decreciente en los intervalos de la
forma (a, b) donde a = π/2
+ 2·k·π y b = 3π/2 + 2·k·π siendo k∈Z .
6) Tiene infinitos máximos relativos
en los puntos de la forma (π/2 + 2·k·π,
1) con k∈Z .
Tiene infinitos mínimos
relativos en los puntos de la forma (3π/2 + 2·k·π, - 1)
con k∈Z .
7) Es periódica de
periodo 2π .
sen (x) = sen (x + 2π)
La
función f(x) = sen (k·x) es periódica de
periodo p = 2π/k
Para |k|>1 el
periodo disminuye y para 0 < |k| <1 el
periodo aumenta.
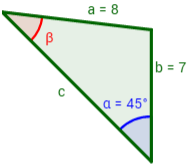
Ejemplos:
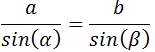
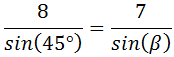
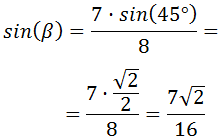
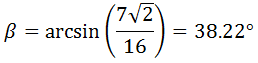
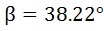



No hay comentarios:
Publicar un comentario