ECUACIONES DE PRIMER GRADO
 Una ecuación de primer
grado o ecuación lineal es una igualdad que involucra una o más variables a la
primera potencia y no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera
potencia.
Una ecuación de primer
grado o ecuación lineal es una igualdad que involucra una o más variables a la
primera potencia y no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera
potencia.
Ecuación de primer grado y una variable

En todo anillo conmutativo pueden definirse ecuaciones de primer grado.
Para resolver las ecuaciones de primer grado se deben seguir los
pasos que se señalan a continuación:
1. Se reducen los términos similares, cuando sea posible.
2. Se realiza la transposición de términos (se aplica la
inversa aditiva o multiplicativa), donde aparezca la incógnita se ubica del
lado izquierdo y los que no la tenga en la derecha.
3. Se reducen los términos similares, en la medida de lo
posible.
4. Se despeja la incógnita, aplicando cociente a
los dos factores de la ecuación por el coeficiente de la incógnita (inverso
multiplicativo) y se simplifica.
En una incógnita
Una ecuación de una variable definida
sobre un cuerpo ,
es decir , con
definida
sobre un cuerpo ,
es decir , con  donde x es la variable, admite la siguiente solución:
donde x es la variable, admite la siguiente solución:
 definida
sobre un cuerpo ,
es decir , con
definida
sobre un cuerpo ,
es decir , con  donde x es la variable, admite la siguiente solución:
donde x es la variable, admite la siguiente solución:
Cuando tanto la incógnita como los
coeficientes son elementos de un anillo que no es un cuerpo, el asunto es más
complicado ya que sólo existirán soluciones cuando m divide a n, si el anillo es un dominio de integridad:

En dos incógnitas
En el sistema cartesiano representan rectas. Una forma común
de las ecuaciones lineales de dos variables es:

Donde representa
la pendiente y el valor de determina el punto
donde la recta corta al eje Y (la ordenada al origen).
Algunos ejemplos de ecuaciones lineales:


Ecuación
lineal en el espacio n-dimensional
Las ecuaciones lineales de varias variables admiten
también interpretaciones geométricas, cuando los coeficientes de la ecuación
pertenecen a un cuerpo. Así una función lineal de dos variables de la forma
siguiente:

representa una recta en un plano. En varias variables asumiendo que tanto
las variables y
los coeficientes ,
donde es un
cuerpo entonces una ecuación lineal como la siguiente:

representa
un hiperplano de n-1
dimensiones en el espacio vectorial n-dimensional .
Sistemas
de ecuaciones lineales
Los sistemas de ecuaciones lineales expresan
varias ecuaciones lineales simultáneamente y admiten un tratamiento matricial.
Para su resolución debe haber tantas ecuaciones como incógnitas y el determinante de la matriz ha de ser
real y no nulo. Geométricamente corresponden a intersecciones de líneas en un
único punto (sistema lineal de dos ecuaciones con dos incógnitas), planos en
una recta (dos ecuaciones lineales de tres incógnitas) o un único punto (tres
ecuaciones lineales de tres incógnitas). Los casos en los que el determinante
de la matriz es nulo no poseen solución.

Si se consideran n ecuaciones de
primer grado linealmente independientes definidas sobre un cuerpo entonces
existe solución única para el sistema si se dan las condiciones del teorema de Rouché-Frobenius, que puede ser
calculada mediante la regla de
Cramer que es aplicable a cualquier cuerpo. Si las ecuaciones
no son linealmente independientes o no se dan las condiciones del teorema la
situación es más complicada. Si el sistema se plantea sobre un anillo conmutativo que no sea un cuerpo,
la existencia de soluciones es también más complejas.
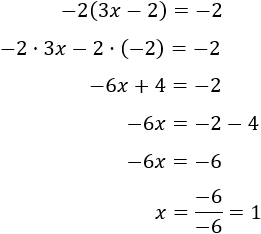

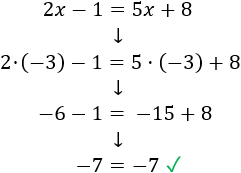

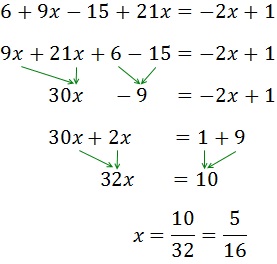
No hay comentarios:
Publicar un comentario